Arnold Sunrise Problem

In a interview in 1995 the notable Russian mathematician Vladimir Igorevich Arnold  recalled a problem set  by his schoolteacher, I. V. Morozkin, when he (Arnold) was 11 or 12 years old. (An Interview with Vladimir Arnold)

“Two old women started at sunrise and each walked at a constant velocity. One went from A to B and the other from B to A. They met at noon and, continuing with no stop, arrived respectively at B at 4 p.m. and at A at 9 p.m. At what time was the sunrise on this day?”

Arnold says “I spent a whole day thinking on this.”  I presume, from Arnold’s statement, the sunrise problem was an extension problem  set for high achievers after they completed  routine exercises.  That Arnold spent a day thinking about the problem implies Mr Morozkin did not teach the class a technique to solve it. Even as an extension exercise the sunrise problem seems far beyond the curriculum for 11-12 year olds in most countries now or then. The year was 1949.  

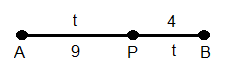
The sunrise problem seems to require fairly advanced abstract thinking at an age when Piaget believed that children were just making the transition from the concrete operational stage of development to the formal operation stage. Arnold said his solution was based on what  are “now called scaling arguments” and “came as a revelation.”  Did he draw something like this?

The women (lets us call them Ekaterina and Yelena) are walking at constant velocity.

Using Arnold's hint we can write V_E = kV_Y. 

Rearranging, k= V_E /V_Y .

Then from the diagram, or otherwise,  t/9 = 4/t.  Obviously, t = 6.

Sunrise occurs 6 hours before noon, that is  06.00 or 6 am.

Actually, I have omitted one step. (AP/t)/(AP/9) = (PB/4)/(PB/t ) But this seems trivial.