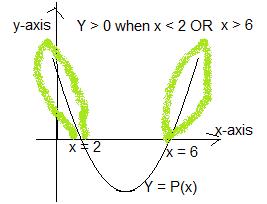Quadratic Functions Test

1.  The equation of a curve is y = 10 – x² + 6x.

 a) Express y in the form a – (x + b) ² , where a and b are integers.                                                

The equation for y in the expanded form = The equation for y in the given form

10 – x² + 6x = a – (x + b) ²

10 – x² + 6x =  a – (x² + 2bx +  b²) ; expand the squared term

10 – x² + 6x =  a –  x² –  2bx –  b²; distribute the  –  sign

– x² + 6x + 10 =  –  x² –  2bx –  b² + a ; order terms by their degree

And match up the coefficients:

– x² =  –  x² ;  6x =  –  2bx  à b = -3;  10 =  –  b² + a à a =10 + b² = 19

b) Hence, find the coordinates of the vertex of the curve.                             

The vertex form is  Y = A(X – H)² + K

The vertex form is also Y =  K + A(X – H) ² by the Commutative Law of Addition (e.g., 2 + 3 = 3 + 2)

Compare with                y = 19 – (x + (-3)) ²

Obviously, K = 19,    and A = -1.

Also – H = +(-3)                     

Therefore H = +3

Hence, the vertex is (x, y) = (H, K) = (+3, +19)

2. Solve the quadratic inequality:   x² – 8x + 12 > 0.     Your answer must include a sketch.  

Let y = P(x) = 1x² – 8x + 12, with a = 1, i.e. a positive number. We have no requirement for b and c.

To find the roots change the form of the polynomial from expanded form to factored form.

y = (x – 6)(x – 2) in factored form

Set y = 0 to find the roots. 

x – 6 = 0 à x = 6

x – 2 = 0 à x = 2.   The roots are “critical numbers” on the x-axis.  Between the roots the parabola is under the x-axis. To the left and right of the roots the parabola lies above the x-axis. Check the original problem.  We need the 2 separate pieces of the parabola above the x-axis.

Using our knowledge of set theory, we can write the solution as {x: x < -2 U x > 6, x is a Real number}.  The solution set is composed of 2 disjoint pieces.

3. Determine the set of values of k for which the equation x² + 2x + k = 3kx – 1 has no real roots.              

As given, this equation is of the form, quadratic function = linear function.

A rough sketch shows that there can be 2, 1 or zero solutions. (The sketch of a quadratic function is a parabola. The sketch of a linear function is a line. Amazing!)

To solve, we bring all the terms to the left.

We need (quadratic) – (line)  = 0  has no real roots. 

New quadratic = 0 has no real roots

Do not make the mistake of believing that in the equation y = x² +2x – 3kx + k + 1that ‘x’ and ‘k’ are both variables!!!  Yes, ‘x’ is a variable, because we can draw an x-axis.  However, k is merely a parameter.

y = 1x² + (2 – 3k)x + (k +1)

y = ax² +            bx + c.

By direct comparison:  a = 1, b = (2 – 3k) and c = (k + 1)

 The phrase “no real roots” should tell you to use the discriminant.

Discriminant = b² – 4ac

D = (2 – 3k) ² – 4(1)(k + 1)

D = 4 – 12k + 9k² – 4k – 4

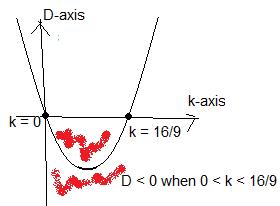
D = 9k² – 16k in expanded form or D = k(9k – 16) in factored form. 

That is, D is a polynomial function of k.  In fact this will also be a parabolic function.

Now, we can give D and k their own axes.

Using set notation the solution is { 0 < k < 16/9}.   Unlike the previous question, all the points in this set form one continuous piece.

Plant Interest

Here is a seedling. It has two leaves which collect sunlight for photosynthesis.  Some of the sugar created is used for the plant’s metabolism and some is used to create DNA, protein, cellulose, et cetera to make new cells and hence new leaves.

 The plant at time ‘zero’.

The plant at week 1.

The plant at week 2.

The plant at week 3.

The plant at week 4.

Time (weeks)	Leaf area (arbitrary units)
0	2
1	3
2	4
3	5
4	6

The plant is adding one new leaf every week.  As it originally had two leaves, its growth rate can be considered to be 50% per week.

To create a formula we will

·         Use the letter P to represent the original number of leaves.  Therefore P = 2.

·         Use the letter R to represent the growth rate.  Therefore R = 50% =  0.5

·         Use the letter T to represent the number of weeks. Therefore 0 <= T <= 4.

·         Use the letter I to represent the number of new leaves. 

·         Use the letter A to represent the total number of leaves. 

Our formula for plant growth is I = PRT. Consequently, A = P + I.

T	I = PRT	A = P + I
0	I = 2 × 0.5 × 0 = 0	A = 2 + 0 = 2
1	I = 2 × 0.5 × 1 = 1	A = 2 + 1 = 3
2	I = 2 × 0.5 × 2 = 2	A = 2 + 2 = 4
3	I = 2 × 0.5 × 3 = 3	A = 2 + 3 = 5
4	I = 2 × 0.5 × 2 = 2	A = 2 + 2 = 4
n	I = 2 × 0.5 × n = n	A = 2 +  n

As you can see, the formula matches perfectly with the observed growth.  Some of you may be saying those formulas look suspiciously like the simple interest formulas for the growth of money in a bank account.  Well, yes.  Actually, these are valuable plants which produce an anti-malarial drug.  Consequently, each leaf can be sold for exactly $1. 00.

End of story?  Not really.  A biologist examines the data. He notices that in week 0 the plant produces 200 units of sugar, i.e. 100 units per leaf.  From the 200 units,  the plant used 150 units for metabolism and 50 units to grow a new leaf.  In succeeding weeks the plant produced much more sugar. However every week the plant only allocated the same 50 units to growth.

T	Sugar produced	Sugar used for metabolism	Sugar used for growth of a new leaf	Percentage of sugar used for growth
0	200	150	50	25%
1	300	250	50	17%
2	400	350	50	13%
3	500	450	50	10%
4	600	550	50	8%
n	200 + 100 n	150 + 100n	50

The biologist notes growth is tending towards 0% as n becomes larger.  Does this not contradict the previous statement that the growth rate R remains at a constant 50% every week? No, because we are ‘comparing apples and oranges.’ The 50% growth rate is in comparison to the original size of the plant. The declining growth rate noted by the biologist is recalculated on a week-to-week basis.

The owner of the plant asks the biologist to use DNA technology to increase the plant’s growth.  After months, or possibly years, of failed experiments, the genetically modified plant grows as follows.

Time (weeks)	Leaf area	Growth on a week by week basis
0	2	n/a
1	3	(3-2)/2 × 100 = 50%
2	4.5	(4.5-3)/3 × 100 = 50%
3	6.75	(6.75-4.5)/4.5 × 100 = 50%
4	10.125	(10.125 - 6.75)/6.75 × 100 = 50%

Some readers may object to the leaf area being given as 4.5 in week 2.  Does this imply ½ a leaf? A moment’s consideration will show there is no cause for concern. The original plant’s leaves were all 10 cm² in size. In the genetically modified plant, most of the new leaves are smaller than the original two leaves, but each leaf still contributes some growth. So in some sense, “Yes, ½ a leaf.”

Financially sophisticated readers will see that the biologist has improved the plant’s yield by causing the plant to switch from a linear growth model to an exponential growth model.

The sequence 2, 4, 6, 8, 10,  … exhibits linear growth. The equation of a line is y = mx + c. This equation is of exactly the same form as A = PI + P. We match y with A, m with P, x with I and c also with P.

The sequence 2, 4, 8, 16, 32,  … exhibits exponential growth. The equation of an exponential curve is y = k×b^x. This equation is of exactly the same form as A = P(1 + r)ⁿ. We match y with A, k with P, (1 + r) with b and x with n. In conclusion, not only is it the case that “time is money” but plant growth is also money! 

Interest

Johnny, Mary, and Ifran each have $100. There are only two banks in town. However, they both offer 5% simple interest.

Johnny puts his money in Ambank for 2 years. Here is what he gets:

 I = PrT

= 100 × 0.05 × 2

= 10

A = P + I

= 100 + 10

=110.

How much would does Mary get if she puts her money in CIMB Bank for 2 years? Obviously, the same amount.

Irfan decides to put his money in Ambank for the first year; then withdrew everything from Ambank and put it in CIMB Bank for the second year.  What does he get?

I_A= P_ArT

= 100 × 0.05 × 1

=5

A_A= P _A + I _A

= 100 + 5

=105

I_C= P_CrT

= 105 × 0.05 × 1

=5.25

A_C = P _C + I _C

= 105 + 5.25

=110.25

Irfan has made a bigger profit than Johnny and Mary have.

Question: Where did the extra 25 cents come from? 

Answer: Compound Interest.

When Johnny kept his money with Ambank for 2 years at simple interest he did not get any benefit from the interest earned in the first year.  That is, he was earning interest on $100 in year 1 and he were still earning interest on the same $100 in year 2. Likewise, for Mary’s money at CIMB. But when Irfan took his money out of Ambank, he started earning interest on $105 in year 2. In other words, in year 2, he was earning interest on the principal and interest on the first year’s interest. Hence ‘compound’ interest.

Now banks don’t want people rushing around at the end of the year withdrawing and depositing money.  Half of the town would take money from bank A and put it in Bank B. The other half would take money out of Bank B and put it in Bank A. Hence, each bank will decide to credit the customer’s account at the end of the year and let him or her earn interest on the principal and interest on the interest.

Is that the end of the story? Not necessarily, suppose a new bank opens up in town and offers monthly interest.  Responding to that threat, another bank offers weekly interest. Where will it stop?