Question
In the regular hexagon below, compare the
shaded area to the entire area.
·
Find the grey area.
·
Find the total area.
·
Compare the two results.
Where to start? It is often a good idea to
make a rough sketch.
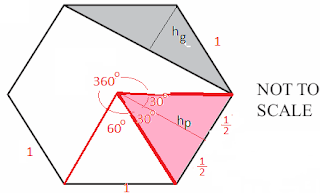
Central congruent triangles
We don’t know if the hexagon has sides of 3
cm or 2 miles or …. Actually it doesn’t
matter. Each of the sides is 1s.
The area of the pink triangle can be found
using A= 1/2
(side)(side) sin
(included angle). Your calculation should show the area of a
pink triangle is √3/4
The grey area
Now consider the grey triangle. The sum of the interior angles is
180(n - 2)°=720°. Therefore one interior angle is 120°. The area of the grey triangle is 1/2 (side)(side) sin (included angle) = 1/2 (1)(1) sin (120°) = √3/4
Solution
The ratio of kX to
X is √3/4 :
6√3/4 so k is 1 ∶
6 = 1/6 .
Aha!
Is the figure below a cube or a
hexagon? Actually we can consider the
hexagon to be the ‘projection’ (or
shadow) of a cube. Immediately, we see the shaded area is one-sixth
|
|
|
|
Input:
A cube(3-D shape) casts a shadow on a wall. Output: A regular hexagon (2-D
shape) is partitioned into 6 congruent triangles. Thanks to students S.H. and A.L. for
partitioning the hexagon into congruent triangles.
|
|






No comments:
Post a Comment