In a interview in 1995 the notable Russian
mathematician Vladimir Igorevich Arnold recalled
a problem set by his schoolteacher, I.
V. Morozkin, when he (Arnold) was 11 or 12 years old. (An Interview with Vladimir Arnold)
“Two old women started at sunrise and each walked at a
constant velocity. One went from A to B and the other from B to A. They met at noon
and, continuing with no stop, arrived respectively at B at 4 p.m. and at A at 9
p.m. At what time was the sunrise on this day?”
Arnold says “I spent a whole day thinking on this.” I presume, from Arnold’s statement, the sunrise problem was an extension problem set for high achievers after they completed routine exercises. That Arnold spent a day thinking about the
problem implies Mr Morozkin did not teach the class a technique to solve it. Even
as an extension exercise the sunrise
problem seems far beyond the curriculum for 11-12 year olds in most
countries now or then. The year was 1949.
The sunrise problem
seems to require fairly advanced abstract thinking at an age when Piaget believed
that children were just making the transition from the concrete operational stage
of development to the formal operation stage. Arnold said his solution was based
on what are “now called scaling arguments”
and “came as a revelation.” Did he draw
something like this?
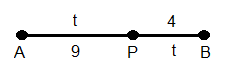
The women (lets us call them Ekaterina and Yelena) are
walking at constant velocity.
Using Arnold's hint we can write VE = kVY.
Rearranging,
k= VE /VY .
Then from the diagram, or otherwise, t/9 = 4/t. Obviously, t = 6.
Sunrise occurs 6 hours before noon, that is 06.00 or 6 am.
Actually, I have omitted one step. (AP/t)/(AP/9) = (PB/4)/(PB/t
) But this seems trivial.