The Pentagram

The pentagram is an ancient symbol (http://mathworld.wolfram.com/Pentagram.html) , recently popularized by Dan Brown (http://www.danbrown.com/the-davinci-code/).   Mathematicians have analysed its properties since the time of Pythagoras.  (www.math.tamu.edu/~dallen/history/pythag/pythag.html)

One such question is what is the area of the blue star below?

 Johnny decides to find the area of the large pentagon (ABCDE) and to subtract the area of the five (congruent isosceles) triangles, each coloured light brown above. ABF is one such triangle.

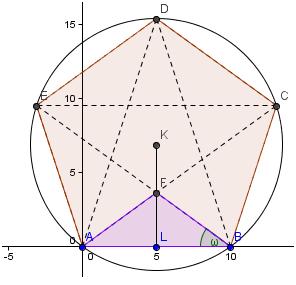
The exterior angle of a regular pentagon is 360°/5 = 72°. Hence each interior angle is 180° - 72° = 108°.  Angle EAB is one such angle so <EAB = 108°.  Call the centre of the pentagon K. Segment KA bisects angle EAB. Hence Angle KAB = ½ ×108° = 54°.

The area of the pentagon is 5 times the area of the green triangle.  The height  of the required triangle is 5 tan 54° = 6.88190…. Hence the area of the triangle is ½ (10)( 6.88190….) = 34.40954. The area of the entire pentagon is 5×34.40954. = 172.047.

                                                                           Each base angle of the highlighted isosceles triangle is ½ (180° -108°) = 36°.Hence, the height of the highlighted triangle is 5 tan 36° = 3.632712. Consequently  the area of the triangle is ½ (10)( 3.632712….) = 18.163563.  The area of all five triangles  is 5×34.40954. = 90.81781.

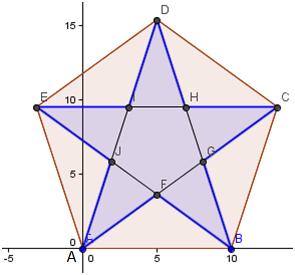
The area of the star is the area of the area of pentagon (ABCDE) minus the area of the five triangles; 172.047 - 90.817 = 81.2 units² to 3 sig figs.

Mary takes a different approach.  She decides the area of the star is five times the area of the dart KAFB (shaded grey below).  A dart is simply an unusual kite.

The area of a kite is half the product of the diagonals = ½ (AB)(KF). Note that diagonal KF is inside the polygon and diagonal AB is outside the polygon; nevertheless the formula still holds. Diagonal AB is given (10 units). Hence, Mary only needs the length of segment KF =  5 tan 54°-  5 tan 36° = 5(tan 54°-   tan 36°) = 6.88190 - 3.632712 = 3.249188.

Mary calculates the area of the star = 5×½ (10)( 3.249188)= 25×3.249188 = 81.2 units² to 3 sig figs.

Conclusion: Johnny and Mary both used the five-fold symmetry of the shape, both used the trigonometric ratio ‘tangent θ’, and both used the same angles (54° and 36°).  Hence their algebra is essentially the same. They only differed in the physical meaning they gave to the algebra. Johnny calculated the area of two triangles (ABK and ABF) whereas Mary calculated the area of the dart KAFB.  

Can you find another way to find the area of the star? Is it possible to find the area but avoid using trigonometry?  What about the mysterious number phi (http://en.wikipedia.org/wiki/Golden_ratio ).