Simultaneous Equations

Mary and Johnny are asked to find the points of intersection of the line x + 5y = 17 with the curve x² + 5y² = 49.

Johnny uses a free dynamic geometry package (Geogebra, download from www.geogebra.org)

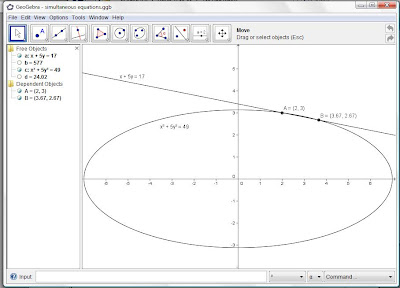
to see that the curve is an ellipse intersected by the line at two points. Note that Point B is rounded to 2 decimal places.

A zoomed in view:

Mary rearranges the equation of the line to get x = 17 – 5y, which she substitutes into the equation of the ellipse.

x² + 5y² = 49

(17 – 5y)² + 5y² = 49

289 – 170 y + 25 y² + 5y² = 49

30y² – 170 y + 240 = 0

3y² – 17 y + 24 = 0

(3y – 8) (y – 3) = 0

y = 8/3 or y = 3

She puts these values of y back into x + 5y = 17

When y = 3, x = 2

When y = 8/3, x = 11/3

Her answer agrees with Geogebra that the points of intersection are A (2, 3) and B (3.67, 2.67). 

___________________________________________________________________________

Examples

1. Solve the simultaneous equations:

x + y = 3 (1)

x² + y² = 29 (2)

2. Solve the simultaneous equations:

y – x = 3 (1)

xy = 4 (2)

3. Solve the simultaneous equations:

2x + 3y = 14 (1)

xy = 4 (2)

4. The line y = 3x – 1 intersects the curve 11 = 2x² + 2y² – x + y at A and B.

Find the co-ordinates of A and B.

5. The line 4x – 3y = 15 intersects the curve 45 = 8x² – 27y² at A and B.

Find the co-ordinates of A and B.

6. The line x – 3y = ^-1 intersects the ellipse 2(x – y) = 2x² – 11y² at A and B.

Find the co-ordinates of A and B.