1. The equation
of a curve is y = 10 – x2 + 6x.
a) Express y in the form a
– (x + b) 2 , where a and b are
integers.
The equation for y in the expanded form = The equation
for y in the given form
10 – x2 + 6x = a – (x
+ b) 2
10 – x2 + 6x = a – (x2 + 2bx
+ b2) ;
expand the squared term
10 – x2 + 6x = a –
x2 – 2bx
– b2; distribute
the –
sign
– x2 + 6x + 10 = – x2
– 2bx – b2 + a ; order terms by
their degree
And match up the coefficients:
– x2 = – x2
; 6x = –
2bx à b = -3; 10
= –
b2 + a à a
=10 + b2 = 19
b) Hence, find
the coordinates of the vertex of the curve.
The vertex form is
Y = A(X – H)2 + K
The vertex form is also Y = K + A(X – H) 2 by the Commutative
Law of Addition (e.g., 2 + 3 = 3 + 2)
Compare with y = 19 – (x + (-3))
2
Obviously, K = 19,
and A = -1.
Also – H = +(-3)
Therefore H = +3
Hence, the vertex is (x, y) = (H, K) = (+3, +19)
2. Solve the quadratic inequality: x2 –
8x + 12 > 0. Your answer must
include a sketch.
Let y = P(x) = 1x2 –
8x + 12, with a = 1, i.e. a positive number. We have no requirement for b and
c.
To find the roots change the form of the polynomial
from expanded form to factored form.
y = (x – 6)(x – 2) in factored form
Set y = 0 to find the roots.
x – 6 = 0 à x
= 6
x – 2 = 0 à x
= 2. The roots are “critical numbers”
on the x-axis. Between the roots the
parabola is under the x-axis. To the left and right of the roots the parabola
lies above the x-axis. Check the original problem. We need the 2 separate pieces of the parabola
above the x-axis.
Using our knowledge of set theory, we can write the
solution as {x: x < -2 U x > 6, x is a Real number}. The solution set is composed of 2 disjoint
pieces.
3. Determine the set of values of k for which
the equation x2 + 2x + k = 3kx – 1 has no real roots.
As given, this equation is of the form, quadratic
function = linear function.
A rough sketch shows that there can be 2, 1 or zero
solutions. (The sketch of a quadratic function is a parabola. The sketch of a
linear function is a line. Amazing!)
To solve, we bring all the terms to the left.
We need (quadratic) – (line) = 0
has no real roots.
New quadratic = 0 has no real roots
Do not make the mistake of believing that in the
equation y = x2 +2x – 3kx + k + 1that ‘x’ and ‘k’ are both
variables!!! Yes, ‘x’ is a variable,
because we can draw an x-axis. However,
k is merely a parameter.
y = 1x2 + (2 – 3k)x + (k +1)
y = ax2 + bx + c.
By direct comparison:
a = 1, b = (2 – 3k) and c = (k + 1)
The phrase “no
real roots” should tell you to use the discriminant.
Discriminant = b2 – 4ac
D = (2 – 3k) 2 – 4(1)(k + 1)
D = 4 – 12k + 9k2 – 4k – 4
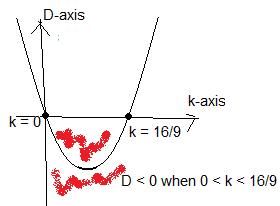
D = 9k2 – 16k in expanded form or D = k(9k
– 16) in factored form.
That is, D is a polynomial function of k. In fact this will also be a parabolic
function.
Now, we can give D and k their own axes.
Using set notation the solution is { 0 < k <
16/9}. Unlike the previous question,
all the points in this set form one continuous piece.



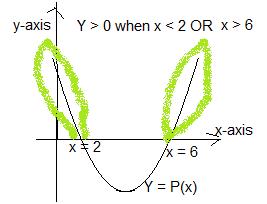

No comments:
Post a Comment