What is a vector? By definition it is something that has a magnitude (length) and a direction (or bearing) but no fixed position. Hard to imagine? Then try the applet below:
Saturday, November 6, 2010
Area of a Parallelogram – The Hard Way
Nixon as a young boy, long before he became President, was a Quaker and evidently his parents told him to never take the easy way of doing any task. How well he applied that advice is best left for historians. This is a maths investigation.
The easy way to find the area of a parallelogram is simply multiply the base times the height, just as you would do for a rectangle. A justification - though perhaps not a 'proof'- is offered pictorially below. Please note that by height, I most definitely do not mean the slant height, but the height that is perpendicular to the base.
In a slightly more difficult method we make use of the substitution:
height = slant height × sin Θ.
The overall formula for the area of the partallelogram is now the still very reasonable:
Area = base × (slant height × sin theta). Again the justification – for those who know a little trigonometry- is a picture.
And then, there is the following complication!
The parallelogeram is formed by the vector addition u + v. The coordinates of u are (a, c) and the coordinates of v are (b, d). The entire shape is a rectangle. To find the area of the parallelogram we will cut away two triangles and two trapeziums. Note that the diagonal of the parallelogram separates the diagram into two congruent halves.
parallelogram = rectangle – 2 congruent triangles – 2 congruent trapeziums
= (a + b) × (c + d) – 2 × ½ (bd) – 2 × ½ [(a + b) + b ] c
(ac + ad + bc + bd) – bd – (a + 2b)c
= ac + ad + bc + bd – bd – ac – 2bc
= ad – bc (Q.E.D. Is sometimes put here. Originally Q.E.D. was short for quod erat demonstrandum, which means "That which was to be demonstrated," although I prefer the somewhat cheeky, “Quite Easily Done.”)
The matrix M is made from u and v written as column vectors
The determinant of the matrix is, det M = product of main diagonal – product of off main
det M = ad – bc, which is exactly the area of the parallelogram, thus justifying one description of the determinant of a matrix as being or representing an area scaling factor.
Parabolas and Intersecting Lines
Suppose you have already plotted P1: y = x2 - 3x + 1, but the teacher asks you to find graphically the roots of P2: y = x2 - 4x + 3. What a bother – now you need to plot another parabola. Or do you?
Johnny can rearrange P2 to get an equation of the form: sloped line = parabola already plotted.
| 0 = x2 - 4x + 3 | Given P2 |
| +x =( x2 - 4x + 3) +x | Add 'x' to both sides |
| x = x2 - 3x + 3 | Simplify by collecting ‘x’ terms on the right |
| x - 2 = (x2 - 4x + 3) - 2 | Add '-2' to both sides, i.e., subtract |
| x - 2 = x2 - 3x + 1 | Simplify by collecting constant terms on the right |
| line = given P1 | |
Now Johnny has a sloped line = parabola that he has already graphed
The sloped line has m = 1 and c = -2, so it is easy to draw.
Reading from the graph, the solution to the teacher’s question is x = 1 or x = 3.
As a check, Mary factorises y= x2 - 4x + 3
y = (x – 3) (x – 1)
When y = 0,
x – 3 = 0, so x = 3
or x – 1 = 0 so x = 1
Done!
Saturday, October 30, 2010
The Discriminant
The quadratic equation y = ax2 + bx + c, represents a parabola. Play with the sliders in the geogebra applet to see the effect of positive or negative a, b and/or c. What happens when b2 – 4ac is negative, when b2 – 4ac = 0, or when b2 – 4ac > 0?
Friday, October 29, 2010
Significant Figures and Rounding: Questions & Answers
1. Write down the significant figure specified in the bracket:
a) 47.351 (2nd)
The second s.f. is 7. Note the question asks for the 2nd digit, not two digits. A common mistake
was to round the number to 2 s.f.
b) 0. 01230 (3rd)
The third s.f. is 3. Leading zeros are not mathematically significant, and are simply “place-holders.”
2.Give the following correct to the accuracy given in the brackets:
a) 5972 to 1 s.f. is 6000
b) 809.317 to the nearest 10 is 810
c) 0.04065 to 3 s.f. is 0.0407
d) 0.08374 to 2 d.p. is 0.09, or simply .09
3. To the nearest 100, attendance at the School Carnival was 2300.
a) What is the maximum number who could have attended?
“To the nearest 100” means “plus or minus 50”.
2300 + 50 equals 2350. However this could not have been the actual attendance. If 2350 was the true figure the attendance would have been given as “2400 to the nearest 100.” But it wasn't. So the true maximum must be 2349. (Under the assumption that the commom rounding convention for 5s has been used.)
b) What is the minimum number who could have attended?
The minimum number of people who attended could be 2300 – 50 = 2250.
4. Estimate the following calculations. (Show all workings.)
a) 596 / 9.12 To one s.f. each this becomes 600/10 = 60
b) 16.5 * 14.4 To one s.f. each this becomes 20 * 10 = 200. If you are good with squares you might say its about 15 * 15 = 225.
5. Douglas wants to save RM 1850 by putting the same amount of money into a savings account for 26 weeks.
a) Estimate how much he should save each week. (Show all workings.)
There are several approaches:
1 s.f. each gives RM 2000/30 = 200/3 = 66 --> 70 to 1 s.f.
Or using 2 s.f., note that 26 is close to 25 and that 100 is 4 * 25:
1850/26 ~ 1900/25 = (19 * 4 * 25)/25 = 19*4 = 76
b) Do you think you estimate is too large, too small, or about right? Explain why.
RM 70 is about right, because 70 * 26 = 1820 which is very close to the original figure of RM1850.
Although the $76 estimate seems clever, it actually may not be. Because it is much harder to mentally calculate 76 * 26, you will probably skip this step where you check if your estimate is 'too large, too small, or about right'. Potentially costly, if you accept a caculator answer that is the result of incorrectly keyed in data and/or operations. Two acronyms to remember:
- K.I.S. = Keep It Simple
- G.I.G.O. = Garbage In, Garbage Out
Sunday, October 24, 2010
Polynomials Test
1. Complete the following statement about the factor theorem:
If f(b) = 0, …………………………………….. [1]
2a) The remainder when the expression x3 – 11x2 + kx – 30 is divided by x – 1 is 4 times the remainder when this expression is divided by x – 2. Find the value of the constant k. [4]
b) Solve the equation x3 – 4x2 – 8x + 8 = 0, expressing non-integer solutions in the form a ± √b, where a and b are integers. w07p1q8 [5]
Polynomials: Answers
Johnny and Mary write a test on polynomials.
1. Complete the following statement about the factor theorem:
If f(b) = 0, ……………………………………..
Johnny’s answer: “If f(b) = 0, (x – b) is a factor of f(x)”
Mary’s answer: “If f(b) = 0, f(x) = (x –b) × Q(x)”
Both are correct.
2a) The remainder when the expression x3 – 11x2 + kx – 30 is divided by x – 1 is 4 times the remainder when this expression is divided by x – 2. Find the value of the constant k.
Johnny uses the Remainder Theorem.
The remainder when f(x) is divided by x – 2 = f(2)
r = f(2)
r = 8 – 44 + 2k – 30
r = 2k – 66
Johnny knows two facts about division by (x – 1):
The remainder when f(x) is divided by x – 1 = f(1)
The remainder when f(x) is divided by x – 1 = 4 × f(2) = 4r
4r = f(1)
4r = 1 – 11 + 1k – 30
4r = k – 40
Johnny substitutes for 4r
2k – 66 = k – 40
k = 32
Mary uses long division. She gets the same answer, although her method is not as efficient.
b) Solve the equation x3 – 4x2 – 8x + 8 = 0, expressing non-integer solutions in the form a ± √b, where a and b are integers.
By trial and error, Mary finds P(-2) = 8 – 16 +16 + 8 = 0
Therefore (x – -2) = (x + 2) is a linear factor.
Mary reasons that a cubic equation must have three factors, but reference in the question to “a ± √b” is a very obvious hint that she will need to use the quadratic formula. Hence, she sees no point in continuing to look for other factors by trial and error!
Mary uses Polynomial Identity to find the quadratic factor.
P(x) = x3 – 4x2 – 8x + 8 = (x + 2) (ax2 +bx + c)
1x3 – 4x2 – 8x + 8 = x(ax2 +bx + c) + 2(ax2 +bx + c)
1x3 – 4x2 – 8x + 8 = ax3 +bx2 + cx + 2ax2 +2bx + 2c
1x3 – 4x2 – 8x + 8 = ax3 +(b +2a)x2 + (c +2b)x + 2
Mary knows when two polynomials are identical the coefficient of each term (degree by degree) must be identical.
She equates the third degree terms, 1x3 = ax3
a = 1
She equates the constant (or degree zero) terms, 8 = 2c
c = 4
She substitutes a = 1 and c = 4 into (b +2a)x2 + (c +2b)x
Therefore, b = -6 and the quadratic factor is 1x2 – 6x + 4.
Now Mary uses the quadratic formula.
Her solutions for P(x) = 0 are x = 3 + √5, or x = 3 √5, or x= 2. Excellent work!
Notes: Question 2 is taken from Cambridge International Education IGCSE Additional Mathematics winter 07 paper 1 question 8.
Tuesday, October 19, 2010
Using Geogebra
Geogebra is a mathematics software for learning and teaching.
You can download either a webstart version or an offline version at www.geogebra.org/cms/en/download
Once geogebra is installed you can use geogebra files to learn about a particular topic, such as gradient of a line, vector addition, or 2-D matrix transformations.
Get on-line help, off-line help (as pdf files) or training videos here:
I will (gradually) upload my geogebra files to the geogebra wiki upload manager, here
Hint: Many other teachers (and students) have uploaded materials and they are usually more sophisticated than my own efforts. www.geogebra.org/en/upload/
Click on a *.ggb file to save it to your computer. Then open it with Geogebra and explore!
For example, download my "column vectors.ggb". Move the floating vectors to discover the laws of vector addition and subtraction.
Saturday, October 16, 2010
Why is a Raven like a Writing Desk?
Here's a riddle for you: Why is a Raven like a Writing Desk? Actually I don't know. Although you just might want to read www.straightdope.com/columns/read/1173/why-is-a-raven-like-a-writing-desk .
Here's another riddle: Why is a rabbit population like a sequence of drum beats? And why are both like a special rectangle?
Give up? They are all representations of the Fibonacci sequence which is made up of the numbers 1, 1, 2, 3, 5, 8, 13, ...
Fibonacci was a mathematician who lived in Europe in the Middle Ages. He travelled to north Africa where he learned from Arab scholars how to calculate with Hindu numerals (i.e., 0, 1, 2, 3, ...9). Try the following calculation: LVII x CMIX. Too hard? Its just 57 x 909. However he is most famous for the following problem:
A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive? www-groups.dcs.st-and.ac.uk/~history/Biographies/Fibonacci.html
But what do rabbits have to do with drum beats? Fibonacci invented the rabbit problem for his students in 1202 AD. But two Indian mathematicians have a prior claim: Gopāla, before 1135 AD and Hemachandra, about 1150 AD. Let a long beeaat = 2 short beats. Then: Bn+1 = Bn + Bn-1
| | 1 beat | 2 beats | 3 beats | 4 beats |
| | S | L | L + S = LS | LS+S = LSS |
| | | SS | SS +S = SSS | SSS+S= SSSS |
| | | | S +L = SL | SL+S= SLS |
| | | | | L+L =LL |
| | | | | SS+L=SSL |
| total | 1 | 2 | 3 | 5 |
The next number of beats equals, FIRSTLY all the beats 'alive' in the column previously - add one short beat to the end of these sequences- plus, SECONDLY all of the beats 'alive' two columns previously - add one long beat to the end of those sequences. All 5 beats of length four can become beats of length five by putting a short beat at the end. All 3 beats of length three can also become beats of length five by putting a long beat at the end. Consequently, there must be a total of 8 beats of length five! Indian poets and drummers speak of 'Hemachandra numbers', not 'Fibonacci numbers.' http://www.sju.edu/~rhall/mathforpoets.pdf
There are many other Fibonacci (or Hemachandra) mysteries to explore. Here is just one more. Draw a square of length 1.
Boring! Draw another square of the same size beside it.
A little better. Continue with a square of length 2 above those.
Eventually.
Nature and artists can create spirals and other amazing patterns from these golden rectangles.
the golden spiral below is available at http://demonstrations.wolfram.com/LogarithmicSpiral/
You can download a free Mathematica player for this applet (and hundreds of others) here:
Are you surprised that the same mathemartics underlies such different topics as population biology, drumming and visual art? Galileo wasn't. To him it was no coincidence, because: "Mathematics is the language with which God has written the universe."
Saturday, October 2, 2010
Solutions for Simultaneous Equations
1. Solve the simultaneous equations:
x + y = 3 (1)
x2 + y2 = 29 (2)
Re-arrange (1) as x = 3 – y
Then y2 = 9 – 3y – 3y + y2
Therefore x2 + y2 = (9 – 6y + y2)+ y2 = 29
2y2 – 6y + 9 – 29 = 0
2y2 – 6y – 20 = 0
y2 – 3y – 10 = 0
(y – 5) (y + 2) = 0
y = 5 or y = - 2
When y = 5, x = 3 – y When y = 5, x = 3 – y
x = 3 – 5 x = 3 – - 2
x = -2 x = 5
The solutions are (-2, 5) and (5, -2).
Note: (1) is a line. (2) is a circle centred on the origin with radius √29. The solutions are reflections in y = x.
2. Solve the simultaneous equations:
y – x = 3 (1)
xy = 4 (2)
Multiply both sides of (1) by x: xy – x2 = 3x
Substitute y = 4/x into (1), to get: 4(x/x) – x2 = 3x
x2 +3x – 4 = 0
(x + 4) (x – 1) = 0
x = -4 or x = 1
When x = -4, y = -1
When x= 1, y = 4
The solutions are (-4, -1) and (1, 4).
Note: (1) is a line. (2) is a hyperbola. The solutions are reflections in y = -x.
3. Solve the simultaneous equations:
2x + 3y = 14 (1)
xy = 4 (2)
Multiply both sides of (1) by x: 2x2 +3xy = 14x
Substitute y = 4/x into (1), to get: 2x2 +12(x/x) = 14x
2x2 +12 – 14x = 0 (We can divide both sides by 2. Remember 0/2 = 0)
x2 – 7x + 6 = 0
(x – 6) (x– 1) = 0
x = 6 or x = 1
When x = 6, y = 4/6 = 2/3
When = 1, y = 4
4. The line x – 3y = -1 intersects the ellipse 2(x – y) = 2x2 – 11y2 at A and B.
Find the co-ordinates of A and B.
Re-arrange the equation of the line to get, x = 3y – 1
Then x2 = 9y2 – 3y – 3y + 1
x2 = 9y2 – 6y + 1
Re-arrange the equation of the ellipse to get 2y – 2x + 2x2 – 11y2 = 0.
2y –2(3y – 1) + 2(3y – 1)2 – 11y2 = 0
2y – 6y + 2 + 2 (9y2 – 6y + 1 ) – 11y2 = 0
2y – 6y + 2 + 18y2 – 12y + 2 – 11y2 = 0
18y2 – 11y2 + 2y – 6y – 12y + 2 + 2 = 0
7y2 – 16y + 4 = 0
(7y – 2) (y – 2) = 0
7y – 2 = 0 or y – 2 = 0
y = 2/7 or y = 2
x = 3y – 1 x = 3y – 1
x = 3(2/7) – 1 x = 3(2) – 1
x =– 1/7 x = 5
The points of intersection are A(-1/7, 2/7) and B (5, 2)
Find the co-ordinates of A and B.
Rearrange 4x – 3y = 15 to make y the subject of the equation:
3y = (4x – 15)y = (4x – 15)/3
Therefore y2 = (16x2 – 120 x + 225)/9
Substitute into the curve:
45 = 8x2 – 27 (16x2 – 120 x + 225)/9 0 = 8x2– 3 ( 16 x2 – 120 x + 225 ) – 45
0 = 8x2 – 48x2 – 675 – 360 x – 45
40x2 + 360 x+ 720 = 0
x2 + 9x + 18 = 0
(x + 6) (x + 3) = 0
x = -6 or x = -3
When x = - 6, y = -13
When x = -3, y = -9
6. The line y = 3x – 1 intersects the curve 11 = 2x2 + 2y2 – x + y at A and B.
Find the co-ordinates of A and B.
Square y = 3x – 1 to get y2 = 9x2 – 6x + 1, and substitute into the equation of the curve:
11 = 2x2 + 2(9x2 – 6x + 1) – x + 3x – 1
0 = 2x2 + 18x2 – 12x + 2 – x + 3x – 1 – 11
0 = 20x2 – 10x – 10 (We can divide both sides by 20. )
0 = 2x2 – 1x – 1
(2x + 1) (x – 1) = 0
x = - ½ or x = 1
When x = - ½, y = -2 ½
When x = 1, y = 2
Simultaneous Equations
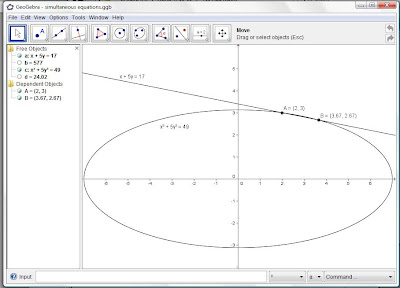
Mary and Johnny are asked to find the points of intersection of the line x + 5y = 17 with the curve x2 + 5y2 = 49.
Johnny uses a free dynamic geometry package (Geogebra, download from www.geogebra.org)
to see that the curve is an ellipse intersected by the line at two points. Note that Point B is rounded to 2 decimal places.
A zoomed in view:
Mary rearranges the equation of the line to get x = 17 – 5y, which she substitutes into the equation of the ellipse.
x2 + 5y2 = 49
(17 – 5y)2 + 5y2 = 49
289 – 170 y + 25 y2 + 5y2 = 49
30y2 – 170 y + 240 = 0
3y2 – 17 y + 24 = 0
(3y – 8) (y – 3) = 0
y = 8/3 or y = 3
She puts these values of y back into x + 5y = 17
When y = 3, x = 2
When y = 8/3, x = 11/3
Her answer agrees with Geogebra that the points of intersection are A (2, 3) and B (3.67, 2.67).
___________________________________________________________________________
Examples
1. Solve the simultaneous equations:
x + y = 3 (1)
x2 + y2 = 29 (2)
2. Solve the simultaneous equations:
y – x = 3 (1)
xy = 4 (2)
3. Solve the simultaneous equations:
2x + 3y = 14 (1)
xy = 4 (2)
4. The line y = 3x – 1 intersects the curve 11 = 2x2 + 2y2 – x + y at A and B.
Find the co-ordinates of A and B.
5. The line 4x – 3y = 15 intersects the curve 45 = 8x2 – 27y2 at A and B.
Find the co-ordinates of A and B.
6. The line x – 3y = -1 intersects the ellipse 2(x – y) = 2x2 – 11y2 at A and B.
Find the co-ordinates of A and B.
Friday, October 1, 2010
Factorising Polynomials
I ask Johnny to find the factors of the cubic polynomial, f(x) = 1x3 – 2x2 – 7x – 4.
He begins by noting that the highest power of x is 3 or equivalently f(x) is of degree ‘3’ and consequently f(x) must have three factors. He decides to use the factor theorem: If f(α) = 0, then (x – α) is a factor of f(x).
Given that the constant term of f(x) is -4, he chooses ±1, ±2, or ±4 as candidates for α.
Is (x – 1) a factor? f(1) = 1(1)3 – 2(1)2 – 7(1) – 4 = 1 – 2 – 7 – 4 = -13
Is (x + 1) a factor? YES. f(-1) = 1(-1)3 – 2(-1)2 – 7(-1) – 4 = -1 – 2 + 7 – 4 = 0
Is (x – 2) a factor? f(2) = 1(2)3 – 2(2)2 – 7(2) – 4 = +8 – large negative ≠ 0
Is (x + 2) a factor? f(-2) = 1(-2)3 – 2(-2)2 – 7(-2) – 4 = -8 – 8 + 14 – 4 ≠ 0
Is (x – 4) a factor? YES. f(4) = 1(4)3 – 2(4)2 – 7(4) – 4 = 64 – 32 – 28 – 4 = 0
Is (x + 4) a factor? f(-4) = 1(-4)3 – 2(-4)2 – 7(-4) – 4 = -64 – 32 +2 8 – 4 ≠ 0
Having used all of his candidates for α, Johnny has found only two factors for f(x). Because he knows there must be a third factor, he decides to apply polynomial identities.
f(x) = (x +1) (x – 4) (bx + c) = 1x3 – 2x2 – 7x – 4. By inspection of the cubic term, b must equal 1. Inspection of the constant term reveals that c = 1 also.
Johnny’s solution is f(x) = 1x3 – 2x2 – 7x – 4 = (x +1) (x – 4) (x + 1) = (x +1)2 (x – 4).
Mary, in the same class, dislikes ‘guesswork,’ and avoids the factor theorem as much as possible. Like Johnny, she finds (x + 1) using the factor theorem, but thereafter she continues with polynomial long division.
As an aside, if you ever want to check that your long division homework is correct, WolframAlpha can be of assistance: www.wolframalpha.com.
Because the quotient is 1x2 – 3x – 4, she knows that f(x) = (x+ 1) (1x2 – 3x – 4). She factorises the quadratic term using mental maths: x2 – 3x – 4 = (x – 4) (x + 1). She and Johnny are in agreement, f(x) = (x +1) (x – 4) (x + 1) = (x +1)2 (x – 4).
Mr. Patterson gives both students gold stars and assigns a new problem. Solve f(x) = g(x), with f(x) as before and g(x) = x2 – 3x – 4.
Both students agree that f(x) = g(x) ought to be re-written as f(x) – g(x) = 0.
Johnny proposes to work with both polynomials in expanded form and to simplify as follows:
f(x) – g(x) = (1x3 – 2x2 – 7x – 4) – (x2 – 3x – 4)
= 1x3 – 3x2 – 4x
= (x) (x2 – 3x – 4)
= (x) (x – 4) (x + 1).
Mary has a different method. She will work with both polynomials in factored form. Since she recognizes that g(x) is the quotient she calculated earlier, she knows g(x) has common factors with f(x). To make the factorization clearer, she underlines the common factors and rewrites g(x) as g(x) × 1.
Thus f(x) – g(x)
= f(x) – g(x) × 1
= (x +1) (x – 4) (x + 1) – (x +1) (x – 4) (1)
= [(x +1) (x – 4)] [(x + 1) – 1]
= (x +1) (x – 4) (x)
Mary and Johnny both know the zero law, “When the product is zero, at least one of the factors must be zero.” Symbolically, a × b = 0 requires either a = 0 or b = 0.
Consequently they write:
0= (x +1) (x – 4) (x)
0 = x + 1 so x = -1 OR 0 = x – 4 so x = 4 OR 0 = x
Again both students are correct.
For you to solve:
y = f(x) ①
y = 6x – 6 ②
f(x) is still the same cubic polynomial, 1x3 – 2x2 – 7x – 4.
h(x) = 6x – 6 is a binomial of degree one, i.e., it represents a line.
Summing up:
Mary and Johnny’s problem is from Exercise 4.6 of Panpac Additional Mathematics by Ho Soo Theng and Khor Nyak Hiong.
Mary and Johnny are not actual students in my class; they are pedagogical prototypes. For this particular problem, although both students had correct answers, Mary demonstrated competence in a greater variety of mathematical methods.
Subscribe to:
Posts (Atom)